CodeV

5.5-计算路径距离

发表于

在您可以说“沿着路径移动35％”之前，您必须能够评估路径的长度。这就是清单5-6中为您提供的函数和方法。它们返回一个值，以点为单位，表示当前scale的路径范围。

pathLength方法通过对其每个元素迭代应用ElementDistanceFromPoint()函数来计算Bezier路径的长度。此函数使用路径状态（特别是当前点和第一点）返回每个连续路径元素的距离。

这依赖于计算三次或二次贝塞尔曲线的距离和直线距离的三个函数。曲线采样N次; 您可以指定采样号。在这个代码清单中，它是6。这对大多数曲线来说是一个不错的近似。一些实现将该采样数量减少到三个以增加总体效率。这样做的折衷是：你采集的样本越少，距离测量的准确度就越低。

图5-4显示了一个真实世界的例子，其中我计算了三点和六点值之间的差异。每个曲线的结果等于采样点之间的线性距离的总和。在这种情况下，三点样品比六点样品短大约6％。随着曲率增加，采样差异也增加，对于高度弯曲的三次曲线部分则误差高达10％-15％。

图5-4

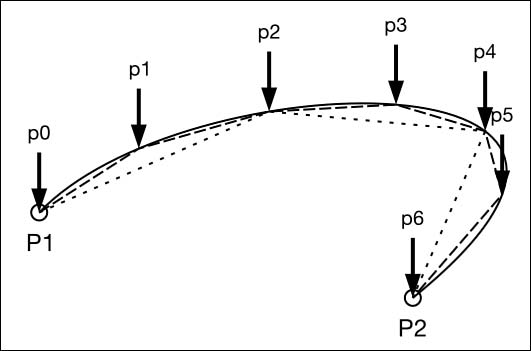
图5-4随着样本段数量的增加，路径长度测量值变得更准确。实线是原始曲线。短虚线使用六个样本来近似测量曲线。点虚线使用三个样本来近似测量曲线。

当然要权衡，随着提高样本数，计算曲线近似的时间增加，测量的精度也随之增加。但是样本太多的话，你只是旋转你的CPU的轮子（比喻CPU重复计算），没有实质的数学改进你的测量方法。

清单5-6 元素间距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
// Distance from p1 to p2
CGFloat PointDistanceFromPoint(CGPoint p1, CGPoint p2)
{
	CGFloat dx = p2.x - p1.x;
	CGFloat dy = p2.y - p1.y;
	return sqrt(dx*dx + dy*dy);
}

// How many points to interpolate
#define NUMBER_OF_BEZIER_SAMPLES 6

// Cubic length
float CubicBezierLength(
	CGPoint start, CGPoint c1, CGPoint c2, CGPoint end)
{
	int steps = NUMBER_OF_BEZIER_SAMPLES;
	CGPoint current;
	CGPoint previous;
	float length = 0.0;
	
	for (int i = 0; i <= steps; i++)
	{
		float t = (float) i / (float) steps;
		current = CubicBezierPoint(t, start, c1, c2, end);
		if (i > 0)
			length += PointDistanceFromPoint(current, previous);
		previous = current;
	}
	
	return length;
}

// Quad length
float QuadBezierLength(
	CGPoint start, CGPoint c1, CGPoint end)
{
	int steps = NUMBER_OF_BEZIER_SAMPLES;
	CGPoint current;
	CGPoint previous;
	float length = 0.0;
	
	for (int i = 0; i <= steps; i++)
	{
		float t = (float) i / (float) steps;
		current = QuadBezierPoint(t, start, c1, end);
		if (i > 0)
			length += PointDistanceFromPoint(current, previous);
		previous = current;
	}
	
	return length;
}

// Calculate element-to-element distance
CGFloat ElementDistanceFromPoint(
	BezierElement *element, CGPoint point, CGPoint startPoint)
{
	CGFloat distance = 0.0f;
	switch (element.elementType)
	{
		case kCGPathElementMoveToPoint:
			return 0.0f;
			
		case kCGPathElementCloseSubpath:
			return PointDistanceFromPoint(point, startPoint);
		
		case kCGPathElementAddLineToPoint:
			return PointDistanceFromPoint(point, element.point);
			
		case kCGPathElementAddCurveToPoint:
			return CubicBezierLength(point,
				element.controlPoint1, element.controlPoint2,
				element.point);
				
		case kCGPathElementAddQuadCurveToPoint:
			return QuadBezierLength(point, element.controlPoint1,
				element.point);
	}
	return distance;
}

// Bezier pathLength property
- (CGFloat) pathLength
{
	NSArray *elements = self.elements;
	CGPoint current = NULLPOINT;
	CGPoint firstPoint = NULLPOINT;
	float totalPointLength = 0.0f;
	
	for (BezierElement *element in elements)
	{
		totalPointLength += ElementDistanceFromPoint( element, current, firstPoint);
		if (element.elementType == kCGPathElementMoveToPoint)
			firstPoint = element.point;
		else if (element.elementType == kCGPathElementCloseSubpath)
			firstPoint = NULLPOINT;
			
		if (element.elementType != kCGPathElementCloseSubpath)
			current = element.point;
	}
	
	return totalPointLength;
}

本文翻译自《iOS Drawing Practical UIKit Solutions》作者：Erica Sadun，翻译：Cheng Dong。如果觉得本书不错请购买支持正版:亚马逊购买传送门，本书所有源代码可在GitHub上下载。译者虽然力求做到信，达，雅，但是由于时间仓促加之译者水平十分有限，文中难免会出现不正确，不准确，词不达意，难于理解的地方，还望各位批评指正，共同进步，谢谢。转载请注明出处。